Important typeclasses

Understanding a typeclass¶

The best way to understand any given typeclass is to find its documentation online, inspect its methods, and look at some instances. This is usually easy with Google, or failing that, Hoogle.

Here is an example, the Semigroup class:

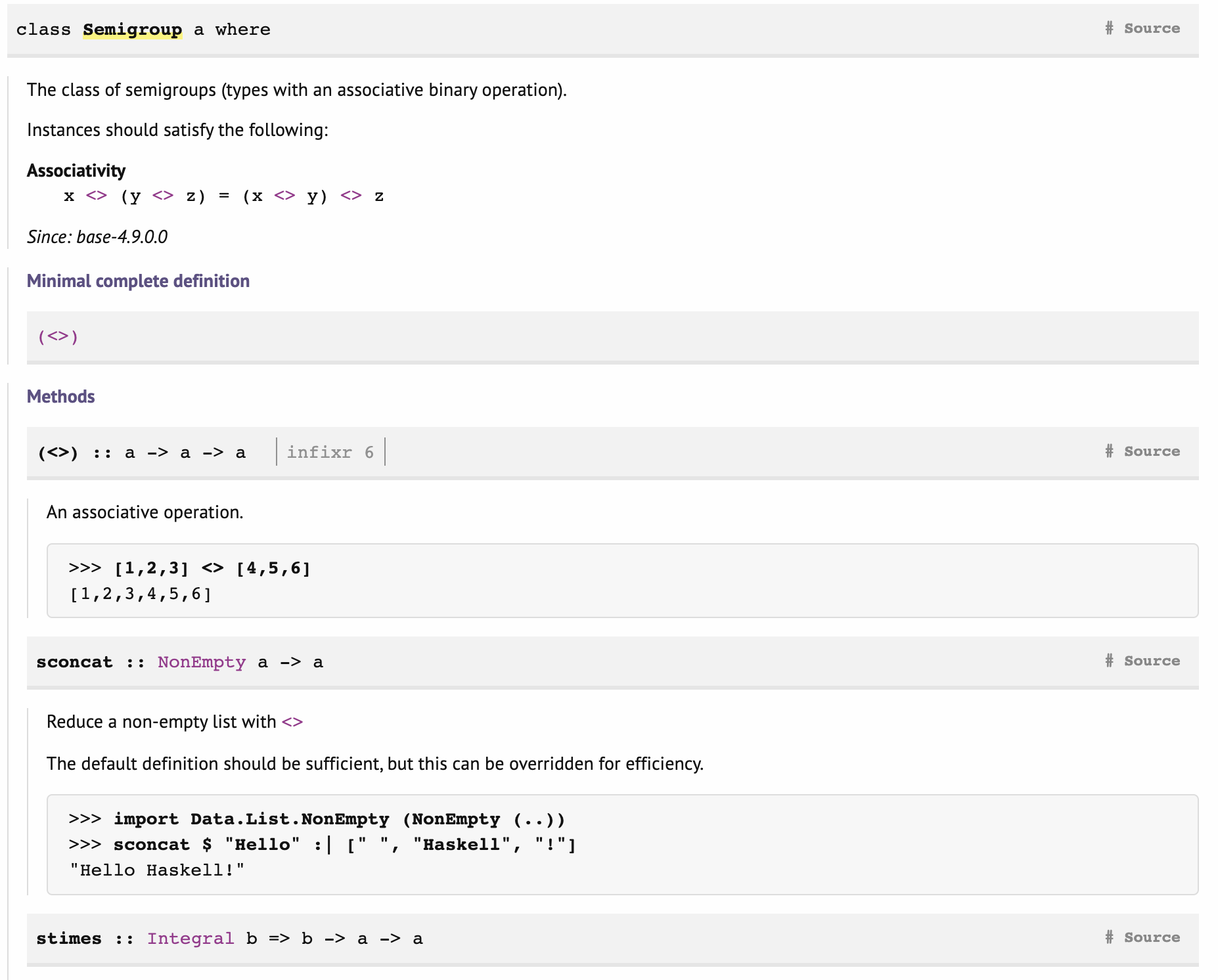
To understand what methods the class requires for its instances, see "minimal complete definition" where (<>) is the only (required) method. See below for its type.

Note

You will also see a comment about associativity, which is a property that instances should have. This property can't be automatically enforced, so is the responsibility of the writer of the instance.

The next step is to inspect some instances, which are also listed below, like:

`:info`¶

The Haskell repl will also provide useful information:

repl example

> :info Num
type Num :: * -> Constraint
class Num a where
  (+) :: a -> a -> a
  (-) :: a -> a -> a
  (*) :: a -> a -> a
  negate :: a -> a
  abs :: a -> a
  signum :: a -> a
  fromInteger :: Integer -> a
  {-# MINIMAL (+), (*), abs, signum, fromInteger, (negate | (-)) #-}

instance Num Word -- Defined in ‘GHC.Num’
instance Num Integer -- Defined in ‘GHC.Num’
instance Num Int -- Defined in ‘GHC.Num’
instance Num Float -- Defined in ‘GHC.Float’
instance Num Double -- Defined in ‘GHC.Float’

Show ¶

A class for converting a type into a String, which can be displayed. String is a legacy type, but Show is widely used, and can be derived by Haskell:

repl example

> data Piece = Bishop | Knight deriving Show
> show Bishop
"Bishop"

Most instances that should exist do exist. For example:

instance Show Int
instance Show Bool
instance Show a => Show [a]
instance Show a => Show (Maybe a)

Gotcha

repl example

> show (+)
"No instance for (Show (Integer -> Integer -> Integer))..."

Haskell won't show arbitrary functions, because they don't have a Show instance. This makes sense, since it is impossible to show all the (infinite) input-output pairs of a function.

Eq ¶

Types which support a notion of equality.

Ord ¶

Types which support a notion of comparison.

Num ¶

Types which support a notion of addition, multiplication and negation. Some laws, like commutativity of addition, are expected to hold.

Semigroup ¶

Provides a method to combine two values: (<>) :: a -> a -> a

Any instance should define <> such that it is associative (i.e. a <> (b <> c) = (a <> b) <> c)

`instance Semigroup Text`¶

repl example

> :set -XOverloadedStrings -- (1)!
> import Data.Text
> text = "hello"
> text2 = "world"
> text <> text2
"helloworld"

See here for explanation of why this is needed.

Monoid¶

Info

For historical reasons (Monoid predates Semigroup), Monoid has a method mappend which is redundant given the inheritance of <> from Semigroup.

The Monoid constraint implies the Semigroup constraint.

class Semigroup a => Monoid a where
  mempty :: a

mempty (short for: monoid empty) is a value of type a.

Examples:

repl example

> mempty :: Any

Any {getAny = False}
> mempty :: All

All {getAll = True}

> mempty :: Product Int -- (1)!
Product {getProduct = 1}

> mempty :: Sum Int
Sum {getSum = 0}

> mempty :: [Int]
[]
> mempty :: [Bool]
[]
> mempty :: [a]
[]

> import Data.Text
> mempty :: Text
""

-- if X has a Monoid instance, so does (Y -> X) for any Y.
> (mempty :: Int -> Text) 4
""
> (mempty :: Int -> Text) 6
""

Product X has a Monoid instance if X has a Num instance.

Functor ¶

with explicit kind signaturewithout explicit kind signature

class Functor (f :: * -> *) where -- (1)!
    fmap :: (a -> b) -> f a -> f b

The kind signature f :: * -> * requires the GHC2021 standard extensions.

class Functor f where
    fmap :: (a -> b) -> f a -> f b

Hint

Types which are instances of Functor must have kind * -> *.

So Int or Bool or Either Int Bool or [Int] cannot be instances of Functor, but Either Int, or [] can. (See section on partial application of types.)

List¶

The definition of fmap for [] is just map

repl example

> ls = [1 :: Int, 2, 3]
> :t ls 
ls :: [Int]
> fmap even ls
[False,True,False]
> :t fmap even ls
fmap even ls :: [Bool]

Maybe¶

repl example

> maybeChar = Just 'a'
> :t maybeChar
maybeChar :: Maybe Char
> fmap (=='a') maybeChar
Just True

> :t fmap (=='a') maybeChar
fmap (=='a') maybeChar :: Maybe Bool

> fmap (=='a') Nothing
Nothing

Either a¶

Note

Either a is Either partially applied to a, and has kind * -> * as required.

repl example

> eitherChar = Right 'a'
> :t eitherChar
eitherChar :: Either a Char -- (1)!
> fmap (=='a') eitherChar
Right True

> :t fmap (=='a') eitherChar
fmap (=='a') eitherChar :: Either a Bool

> other = Left True
> :t other
other :: Either Bool b
> fmap (=='a') other
Left True
> :t fmap (=='a') other
fmap (=='a') other :: Either Bool Bool -- (2)!

Haskell correctly infers that a can be any type.
Haskell correctly infers the type, which is no longer universally quantified.

Reader r¶

newtype Reader r a = Reader {runReader :: r -> a}

So, for example, Reader Int Bool is really just a wrapper around a function Int -> Bool.

Conceptually, think of a Reader env a as a value of type a that has access to (i.e. depends on) a value of type env.

An example:

repl example

> import Control.Monad.Reader -- (1)!
> val = reader -- (2)!
    (\flag -> if flag then "hello world" else "no greeting")
> runReader val True
"hello world"
> runReader val False
"no greeting"

-- example of fmap
> newVal = fmap (take 5) val
> runReader newVal True
"hello"

From the mtl package.
mtl doesn't define Reader exactly as shown above, so use lowercase reader to construct a value of type Reader err a, rather than uppercase Reader.

State s¶

newtype State s a = State {runState :: s -> (a, s) }

So, for example, State Int Bool is really just a wrapper around a function Int -> (Bool, Int).

Conceptually, think of a State st a as a value of type a that requires a value of type s to be obtained, and results in a new value of type s.

Example:

repl example

> val = state (\ls -> if length ls > 3 then (Just (head ls), drop 1 ls) else (Nothing, ls))
> runState val [1,2,3]
(Nothing,[1,2,3])
> runState val [1,2,3,4]
(Just 1,[2,3,4])

-- example of fmap
> import Data.Maybe
> newVal = fmap isJust val
> runState newVal [1,2,3]
(False,[1,2,3])
> runState newVal [1,2,3,4]
(True,[2,3,4])

Applicative¶

class Functor f => Applicative f where
  pure :: a -> f a
  liftA2 :: (a -> b -> c) -> f a -> f b -> f c

repl example

> import Control.Applicative

-- examples with []
> pure 1 :: [Int]
[1]
> liftA2 (+) [1,2,3] [2,3,4]
[3,4,5,4,5,6,5,6,7]
> liftA2 (\x y -> (x,y)) ['a', 'b'] [True, False, True]
[('a',True),('a',False),('a',True),('b',True),('b',False),('b',True)]

-- examples with Maybe
> data Color = Black | White deriving Show
> pure Black :: Maybe Color
Just Black
> liftA2 (+) (Just 3) (Just 4)
Just 7
> liftA2 (+) (Just 3) Nothing
Nothing
> liftA2 (+) Nothing (Just 5)
Nothing


-- examples with Reader
> boringVal = pure True :: Reader Int Bool
> runReader boringVal 4
True
> runReader boringVal 3
True

-- example of liftA2
val = reader (\flag -> if flag then "hello world" else "no greeting")
> combinedVal = liftA2 (<>) val val
> runReader combinedVal True
"hello worldhello world"
> runReader combinedVal False
"no greetingno greeting"

Note

liftA2 and pure can be used to define:

(<*>) :: f (a -> b) -> f a -> f b

and conversely, <*> and pure can be used to define liftA2. For this reason, pure and <*> are also sometimes given as the basic methods of Applicative.

Monad¶

class Applicative m => Monad m where
  (>>=) :: m a -> (a -> m b) -> m b

Note

For legacy reasons, Monad also has a method return, which is a synonym for pure, and is therefore redundant, because all Monad instances are also Applicative instances and so have access to the pure method.

Hint

Compare the type of (>>=) with the type of fmap. In fmap, the function f in fmap f x has type a -> b, but in (>>=), it has type a -> m b.

As a concrete example, consider lists:

fmap :: (a -> b) -> ([a] -> [b])
(>>=) :: (a -> [b]) -> ([a] -> [b])

repl example

-- lists
> upTo5 c = [c .. 5]
> [1,2,3,4] >>= upTo5
[1,2,3,4,5,2,3,4,5,3,4,5,4,5]

> Just True >>= (\x -> if x then Just 1 else Nothing)
Just 1
> Just False >>= (\x -> if x then Just 1 else Nothing)
Nothing
> Nothing >>= (\x -> if x then Just 1 else Nothing)
Nothing

Using do-notation, the first example above becomes:

example = do
    i <- [1,2,3,4]
    pure (upTo5 i)

An illustrative example with State:

example :: State [Int] Bool
example = do
    stack <- get
    let headIsGreaterThan3 = head stack > 3
    if headIsGreaterThan3
        then put (tail stack)
        else pure ()
    return headIsGreaterThan3

-- > runState example [1,2,3]
-- (False,[1,2,3])
-- > runState example [4,2,3]
-- (True,[2,3])

Alternative¶

class Applicative f => Alternative f where
  empty :: f a
  (<|>) :: f a -> f a -> f a

This is like Monoid but for a value of type f a, where f is an instance of Applicative. Parsers are a common use case.

Another is backtracking search which uses the Alternative instance of the Logic monad.

Other instances include Maybe and [].

Important typeclasses

Understanding a typeclass¶

:info¶

Show¶

Eq¶

Ord¶

Num¶

Semigroup¶

instance Semigroup Text¶

Monoid¶

Functor¶

List¶

Maybe¶

Either a¶

Reader r¶

State s¶

Applicative¶

Monad¶

Alternative¶

Comments

`:info`¶

Show ¶

Eq ¶

Ord ¶

Num ¶

Semigroup ¶

`instance Semigroup Text`¶

Functor ¶